Aufgabe:
Text erkannt:
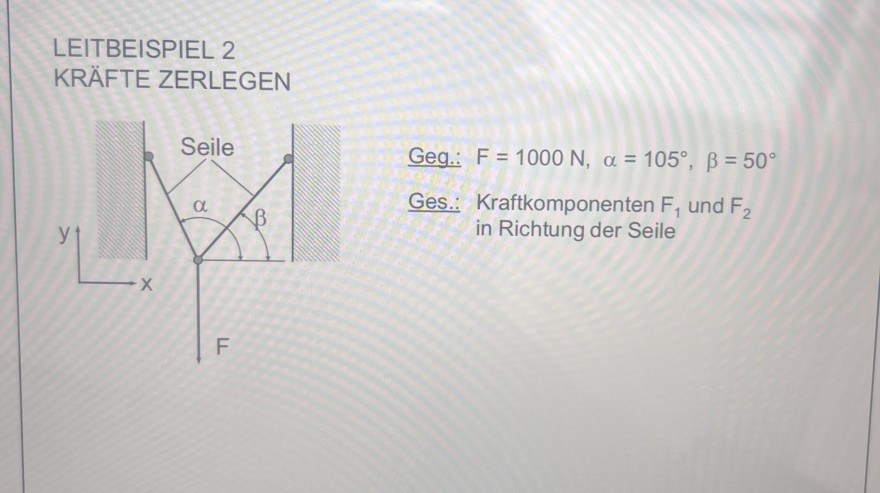
LEITBEISPIEL 2
KRÄFTE ZERLEGEN
Geg.: \( F=1000 N, \alpha=105^{\circ}, \beta=50^{\circ} \)
Ges.: Kraftkomponenten \( F_{1} \) und \( F_{2} \) in Richtung der Seile
Text erkannt:
LEITBEISPIEL 2
KRÄFTE ZERLEGEN
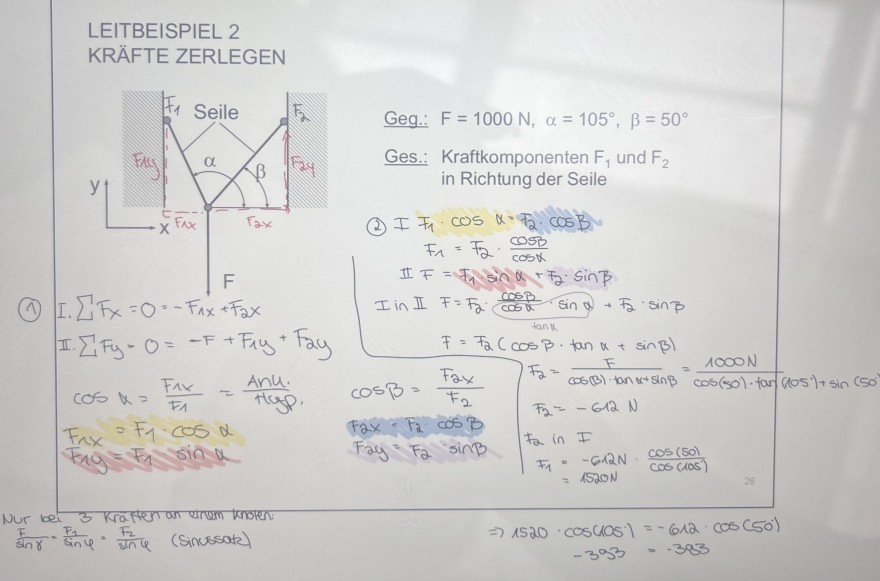
(1) I. \( \sum F_{x}=0=-F_{1 x}+F_{2} x \)
II. \( \sum F_{y}-0=-F_{1}+F_{1 y}+F_{2 y} \)
\( \cos \alpha=\frac{F_{1 x}}{F_{1}}=\frac{\text { Anu. }}{\text { Hosp. }} \text {. } \)
\( F_{n x}=F_{1} \cdot \cos \alpha \)
\( F_{1} g=F_{1} \sin \alpha \)
Geg.: \( F=1000 N, \alpha=105^{\circ}, \beta=50^{\circ} \)
Ges.: Kraftkomponenten \( F_{1} \) und \( F_{2} \) in Richtung der Seile
(2) I \( F_{1} \cdot \cos \alpha=F_{2} \cdot \cos B \)
\( F_{1}=F_{2} \cdot \frac{\cos \beta}{\cos \alpha} \)
II \( F=T_{1} \sin \alpha+F_{2} \cdot \sin \beta \)
I in II \( F=F_{2} \frac{\frac{\cos \beta}{\cos \alpha} \cdot \sin \alpha}{\tan \alpha}+F_{2} \cdot \sin \beta \)
\( F=F_{2}(\cos \beta \cdot \tan \alpha+\sin \beta) \)
Nur be 3 kratten on einem molen
\( \frac{F}{\sin \gamma}=\frac{F_{1}}{\sin \varphi}=\frac{F_{2}}{\sin \varphi} \) (Sincsiate)
\( \begin{aligned} \Rightarrow 1520 \cdot \cos (105) & =-612 \cdot \cos \left(50^{\circ}\right) \\ -393 & =-383 \end{aligned} \)
Problem/Ansatz:
Also bei dem Beispiel geht es um die Statik.
Ich habe die Lösung von meinem Prof bekommen jedoch möchte ich den Weg verstehen.
Mir ist bewusste das die Summe der Kräfte der x und der y-Komponente 0 ergeben sollen.
Wie kommt man aber auf den Rest? Ich bräuchte eine Erklärung was bei den Rechenschritten gemacht wird