Aufgabe:
Ich habe diesen Kegelstumpf gegeben:
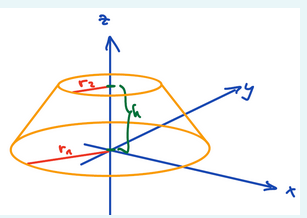
Mit r1 = 0.025m
r2 = 0.011m
h = 0.024m
sowie der Dichtefunktion
\( \rho(\vec{r})=2 \frac{\mathrm{kg}}{\mathrm{cm}^{3}}+1,6 \frac{\mathrm{kg}}{\mathrm{cm}^{4}} x+0,9 \frac{\mathrm{kg}}{\mathrm{cm}^{5}} z^{2} \)
und einer Masse von 79.7 Kilogramm. Ich soll die Koordinaten des Schwerpunkts
\( \overrightarrow{r_{S}}=\left(r_{S, x}, r_{S, y}, r_{S, z}\right) \)
in cm berechnen. Mögliche Ergebnisse für x sind
0.675
0.467
0.571
0.519
0.623
Problem/Ansatz:
Die Formel für den Schwerpunkt ist gegeben durch
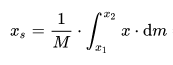
Ich habe x in polarkoordinaten umgewandelt, d.h r*cos(p) und das dann mit der gegebenen Dichtefunktion, ebenfalls in Polarkoordinaten, d.h r*(2+1.6rcos(p) + 0.9z^2), nach dzdrdp integriert:
\( \int \limits_{0}^{-0.583 z+2.5} \int \limits_{0}^{2 \pi} r \cos (p)\left(2+1.6 r \cos (p)+0.9 z^{2}\right) d p d r= \)
\( -0.332012(z-4.28816)^{3} \)
Anmerkung: -0.583z + 2.5 ist der Verlauf von r in Abhängigkeit von z.
\( \int \limits_{0}^{2.4}-0.332012(-4.28816+1 z)^{3} d z=27.0108 \)
Das multipliziert mit 1/79.7 ergibt ein für mich nicht realistisches Ergebnis bzw. ist das Ergebnis keines der möglichen Auswahlen